MSc thesis topics
Topic proposals for 2024-2025 can be found below. Check regularly for updates. Please contact me to schedule a meeting if you are interested in one of these topics.
Climate model emulation with deep generative models
Climate science relies on complex computer models to simulate the Earth’s climate system. These models are computationally expensive and require high-performance computing resources. As a result, they are often too slow to be used in real-time applications, such as climate prediction or extreme event attribution. Emulators are statistical models (often based on deep neural networks) that are trained to approximate the output of a complex computer model. They can be used to make predictions much faster than the original model, and can be used to quantify the uncertainty in the model’s predictions.
In this project, we will explore the use of deep generative models to emulate climate models. Deep generative models are a class of deep neural networks that can learn to generate realistic samples from complex high-dimensional distributions. We will investigate diffusion models and variants to emulate the output of climate models, taking into account the complex spatiotemporal structure of the data. Challenges include the scale and structure of the data and the principled validation of the emulation results.
Contact: Gilles Louppe
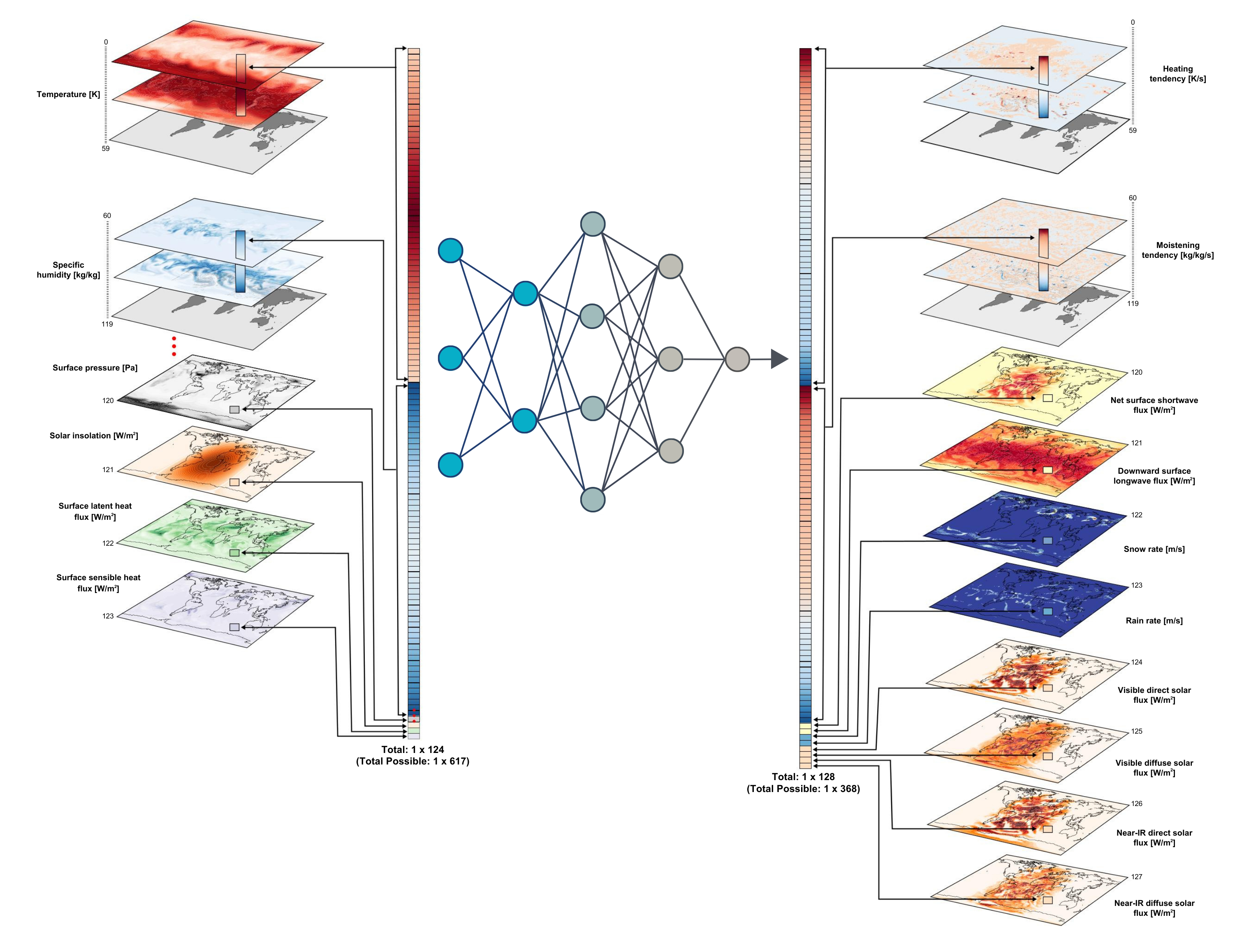
Score-based data assimilation for weather and climate models
Data assimilation is a statistical method used to combine observations with a numerical model in order to estimate the state of a system. In the context of weather and climate models, data assimilation is used to estimate the initial conditions of the model, which are then used to make predictions.
In this work, we will aim to scale score-based data assimilation to high-dimensional and complex models, such as those used in weather and climate science. This work will involve training diffusion models to approximate the prior distribution of a realistic climate system and then exploring realistic observation operators to assimilate real-world observations. Challenges include the scale of the data, the high-dimensional state space, and the principled validation of the assimilation results.
Contact: Gilles Louppe, François Rozet
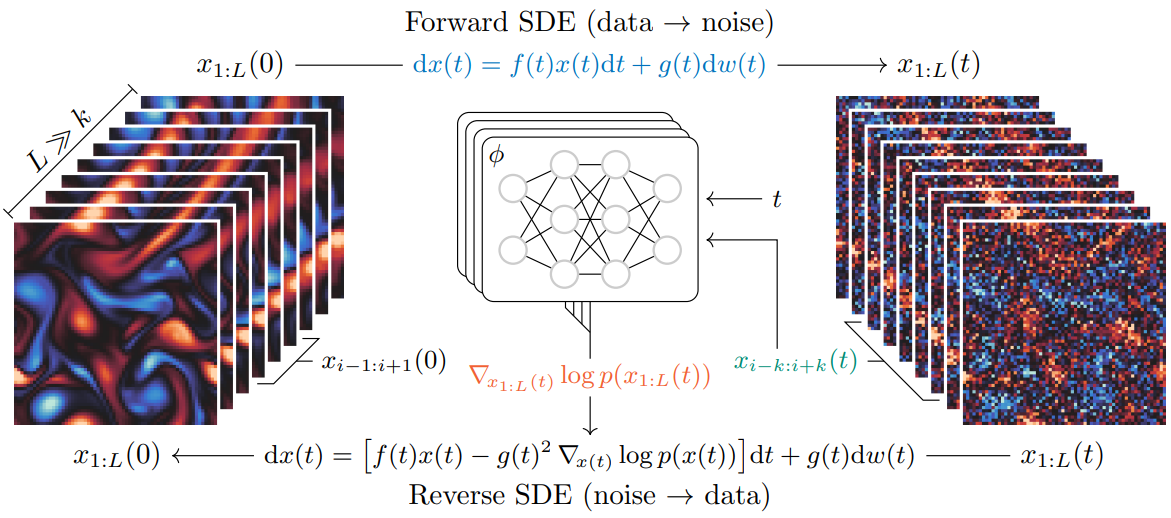
Efficient training of diffusion models
Diffusion models offer a powerful and flexible framework for modeling complex distributions and have shown promise in tasks such as image generation, density estimation, and inverse problems. However, the training of diffusion models can be expensive, both in terms of time and compute, especially in high-dimensional settings. In this work, we will investigate methods for accelerating the training process of diffusion models while maintaining or even improving their performance. This work will involve a review of existing approaches for training diffusion models, a study of the convergence with respect to hyper-parameters (noise schedule, architecture, …) and the development of new methods for fast training of diffusion models.
Contact: Gilles Louppe, François Rozet

Simulation-based inference of neural models from spikes
A fundamental question in neuroscience is how to link observed neural activity to the unobserved biophysical mechanisms that generate this activity. For this reason, there is a critical need for methods to incorporate the partial and noisy data that we observe with detailed, mechanistic models of neural activity.
In this project, we will explore how to estimate the parameters and the hidden variables of neuronal models from neuronal spike train responses. In particular, we will compare modern simulation-based inference methods to more traditional methods like particle filters. Depending on the progress, we will also investigate how to actively collect new data in closed-loop experiments to improve the inference. [PDF]
Contact: Gilles Louppe, Pierre Sacré.

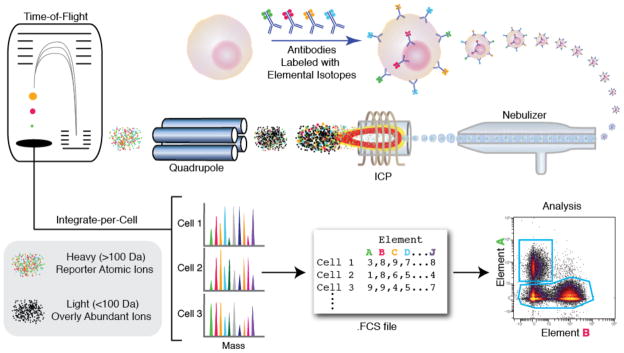
Flow cytometry data analysis with deep learning
Multi-parametric flow cytometry (MFC) is a laboratory technique used to analyze the physical and chemical features of cells. More specifically, flow cytometry data is used to identify and characterize cell populations based on their surface markers and other properties. The analysis of flow cytometry data is complex and requires the use of advanced statistical and machine learning methods. It is widely used in clinical and research settings to study the immune system, cancer, and other diseases.
The first step in MFC consists in mixing cells from a biological sample (e.g., blood) with fluorescently labeled antibodies. The cells are then passed through a laser beam, and the emitted light is collected by detectors. The result is a high-dimensional dataset, where each cell is represented by a vector of measurements, corresponding to the intensity of the emitted light for each of the fluorescent markers. Technological advances have led to an increase in the number of markers that can be measured simultaneously (up to 40 or more) and in the number of cells that can be analyzed (up to millions). This has led to a need for new methods to analyze and interpret the data.
In this project, we will explore unsupervised deep learning approaches to analyze and cluster flow cytometry data. We will investigate deep generative models to learn the underlying structure of the data and to identify subpopulations of cells in control and disease samples, as well as their evolution over time.
Contact: Gilles Louppe, Adrien De Voeght, Frédéric Baron.
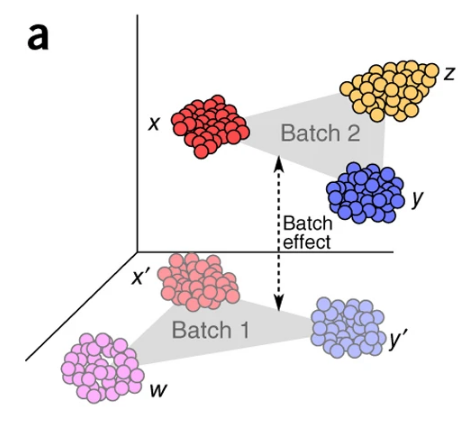
Batch effect correction in single-cell RNA sequencing data with deep learning
Single-cell RNA sequencing is a technology used to measure the expression of genes in individual cells. It is used to study the heterogeneity of cell populations and to identify new cell types. RNA sequencing data is high-dimensional and noisy, and often affected by technical artifacts, such as batch effects, which can confound the biological signal. Batch effects are systematic differences in the measurements of different batches of samples, which can arise from differences in the experimental protocol, reagents, or equipment. Batch effects can lead to spurious associations and can reduce the statistical power of the analysis.
In this project, we will explore machine learning and deep learning approaches to correct batch effects in single-cell RNA sequencing data. We will investigate batch effect correction methods based on deep learning, such as adversarial training or denoising autoencoders to learn batch-invariant representations of the data, and compare them to traditional methods.
Contact: Gilles Louppe, Adrien De Voeght, Frédéric Baron.
Personal research project in deep learning
This thesis proposal is not tied to a specific project. Instead, it welcomes students to make topic proposals on open research problems of their choosing and interest. Proposals should be centered around deep learning. Examples of projects include:
- Theoretical research in deep learning
- Improvements to existing deep learning algorithms or models
- Application of deep learning to solve a real-world problem
- Development of deep learning software
Finding a research problem to work on is considered as part of this thesis subject. Students should come with a concrete and well-defined thesis topic. Proposals will be reviewed and discussed with the student before their approval (if any). [PDF]
Contact: Gilles Louppe.
Deep learning and Computer vision at EVS
In collaboration with EVS Broadcast Equipment, several master thesis topics are proposed on deep learning for sport videos. Topics include novel view synthesis with NeRF, logo detection in sport videos, or generative models for outpainting in sport content, among others. The exhaustive list of projects is available in the document below. [PDF].
Contact: Gilles Louppe, Martin Castin.

Previously supervised MSc thesis (2018-Present) can be found on Matheo.